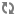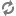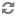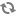3 Reliability and Redundancy
3.1 Reliability
The remote location and the lack of (or expense of) access to any subsea equipment is a major consideration in system design. There are many components and interfaces on a subsea control system that can fail.
There are many reasons for failure. The list below is indicative rather than all encompassing:
Direct Failures: Corrosion, joint failure, splice failure, sensor failure, solenoid valve failure, water ingress, internal control fluid leak, SEM failure (power supply, modem, solenoid driver, control board, etc.), hydraulic coupling leak, hose failure, weld failure, dynamic umbilical fatigue, electrical connection failure.
Indirect Failures: Dropped object, umbilical dragged by anchor chain or trawl board, wax or hydrate blocking sensor port, hydrates blocking HP lines (gas migration from well through HP lines which is cold and at high pressure).
Reliability can be improved by proper burn-in of electronics, and testing, such as shock and vibration. Minor details such as hydraulic coupling seal compatibility should not be overlooked. Electronic components sourced by manufacturers can vary from full 'military' specification, through 'industrial' high or low grade to 'commercial' (household quality) with little visibility or control by the purchaser.
The reliability of any single component that could fail and shut in a field should be questioned. If the component cannot be replaced with a better component, then there should be an alternative redundant path designed into the control system in case of component failure.
Reliability analysis can be a complex task and setting specific reliability targets is often misleading and difficult to verify, requiring clear definition of the sub-systems and the failure modes to be included in the analysis, and the resulting reliability models. A reliability analysis is a statistic analysis of the probability of survival of the system, but it is important to recognise the mathematical basis to this analysis and the meaning of the terms employed, which are sometimes misconstrued to be some form of guarantee that the equipment will survive. For example, the probability of survival Ps of a system over a time it is defined as
Ps(t) = e -λt
where λ = failure rate
t = time
Ps(t) = Probability of survival i.e. reliability
As a corollary of the above:
Pf(t) = 1 - e-λt
Where the parameter MTBF can be defined (for the exponential distribution) as that time at which 36.79% of a given population can be expected to survive, or, alternatively, an individual component has a 36.79% probability of surviving until that time.
MTBF can be calculated as the reciprocal of failure rate (λ)
MTBF = 1/λ
Analysing the models requires the use of established databases, such as MIL-HDBK-217 to obtain the failure rate (λ); these databases, however, are comprehensive for electronic components, but less useful for mechanical and hydraulic components, making a complete analysis difficult to quantify. Setting specific 'minimum component MTBFs ' is therefore impractical.
A more realistic approach is to ensure all components used are to a suitably high specification, for example, electronic components used should be to at least 'industrial' grade, rather than 'commercial'. This latter grade, as well as assuring a higher QA level during manufacture, also sets the ambient temperature over which the device operates and a 'commercial' level component may well not be suitable for the temperatures experienced in a system, particularly during land-testing or even when operating inside an enclosure. In addition, the likely physical failure mode of a component or sub-system should be considered (if possible), to ensure the overall system fails in a 'safe' manner.
A more useful figure is that of 'Availability' of the system, which is defined as:
MTBF / (MTBF+MTTR)
Where MTBF = Mean time between failure
MTTR = Mean time to repair
It can be seen from this equation that the shorter the MTTR, the better the overall availability of the system, and it is this parameter which is a far better target of attention during the system design (the value of MTBF is thus not quite so relevant, for example if MTBF is 1000 hours, a 1-hour MTTR gives an availability of 99.9% and an MTBF of 100 hours with the same MTTR gives 99.01%, whereas a 10-hour MTTR gives 99.00% and 90.9% respectively). It can be improved by arranging for a modular design, adequate tooling to facilitate retrieval and replacement, maintaining a reserve of spare modules etc.
A mathematical (statistical) analysis can be employed to calculate the number of spares of any particular sub-element of the system, but in practice this is more influenced by commercial and contractual issues than an analysis, and it is more usual to choose a 'practical' level of spares or instigate a "TVM" (Total Vendor Management) style support contract (to avoid purchasing a large number of spares that may never be utilised).
3.2 Redundancy
The usual method employed to improve the reliability figure is to duplicate those parts of the system considered to be at high risk - i.e. by adding 'redundancy'.
Redundancy has to be considered in terms of complexity and cost. The implementation of dual systems improves the (mathematical) reliability but it should be noted that all systems must eventually be consolidated at some single physical point (e.g. at the Tree Valve actuator, or at a solenoid pilot valve in an SCM) and the failure mode of this consolidation point can sometimes degrades the overall integrity of the system, as in practice a failure at this point might prevent both dual-redundant paths from operating. (A reliability analysis often assumes this single mode has a zero failure rate).
For example, a shuttle valve required for a dual hydraulic system can be stationary at one of its two positions and when called to activate due to a hose failure, the shuttle can jam in position or its O-ring seals can have set in their deformed position and moving the shuttle causes seal failure.
The normal level of a dual redundant control system is as follows:
Within the SCM:
Some manufacturers supply dual electronics as standard to justify the standard of electronic components used.
Common practice on TOTAL recent Deepwater developments (PAZFLOR, CLOV, MOHO NORD, KAOMBO, EGINA) is to have one SCM (on each Xmas tree) with two redundant SEMs fitted inside with between 1 and 3 additional SCMs purchased as capital spares and stored in warehouse.
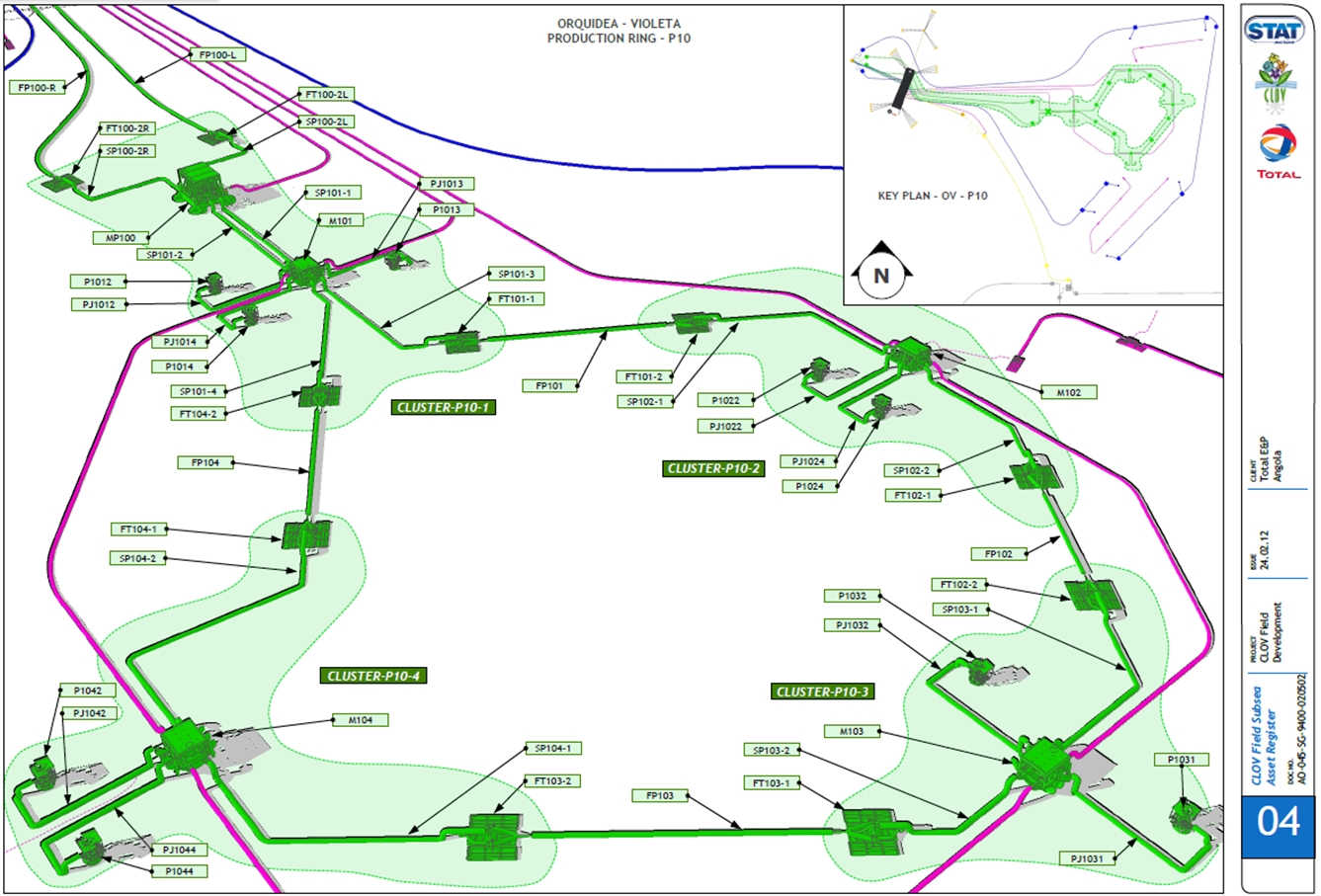
Some Operators require higher levels of redundancy therefore dual umbilicals are sometimes specified. On TOTAL recent Deepwater developments, rather than having duals umbilicals between FPSO and one Manifold, it has been preferred to adopt arrangement of production umbilical in forms of loops (like on CLOV or MHN project). In this arrangement, inside a production loop, only nearest Manifold from FPSO is connected to a dynamic umbilical and a static production umbilical is connected to two inline Manifolds. Such loop arrangement allows operations to be continued in case of major failure of one production static or dynamic umbilical.
The provision of total dual system redundancy also brings corresponding system complexity and increased cost. However system consolidation must end in a single point somewhere, for example at a Xmas tree actuator.
For multi-well systems single point failures in control systems should be eliminated, particularly for 'key' valves that can influence Production, such as Manifold Valves. Whilst the failure of one Well in a multi-well system could be acceptable in terms of loss of production, the inability to operate a Manifold Valve could prevent the production of one Manifold, a production line or a production loop.
Such critical application valves are often operated by two separate Subsea Control Modules. Even adopting such a philosophy, the consolidation method must be examined to avoid common-mode failures. Diverse redundancy has been used in the past, for example an electro-hydraulic system with sequenced hydraulic backup, but these are much less common now that the use of subsea electronics has proven itself over the years.